Príspevky členov Učenej spoločnosti Slovenska
Matematické modelovanie a riadenie systémov neceločíselného rádu
Fakulta baníctva, ekológie, riadenia a geotechnológií Technickej univerzity v Košiciach
Vo svojom výskume sa venujem aplikáciám derivácií a integrálov neceločíselného rádu v modelovaní a riadení procesov. Zaoberám sa hlavne využitím diferenciálnych rovníc neceločíselného rádu na matematické modelovanie lineárnych a nelineárnych systémov, identifikáciou ich parametrov, metódami návrhu parametrov regulátorov neceločíselného rádu a ich analógovou i digitálnou implementáciou. Zaoberám sa aj problematikou adaptívneho riadenia s modelmi neceločíselného rádu a tiež extremálnou reguláciou neceločíselného rádu.
Hlavné výsledky výskumu je možné rozdeliť do nasledujúcich blokov:
i) metódy pre numerické riešenie diferenciálnych rovníc neceločíselného rádu, kde okrem rekurentných vzťahov pre riešenie diferenciálnych rovníc boli navrhnuté
aj aproximačné metódy v diskrétnej oblasti,
ii) základné otázky súvisiace so stabilitou systémov neceločíselného rádu, pričom okrem klasickej bola rozpracovaná aj robustná stabilita,
iii) metódy identifikácie dynamických systémov neceločíselného rádu, ktoré využívajú nové prístupy ako napríklad úplnú metódu najmenších štvorcov alebo Mittag-Lefflerovu funkciu,
iv) metódy pre návrh parametrov regulátorov neceločíselného rádu, pričom ide hlavne o metódu umiestnenia pólov, metódu využívajúcu Bodeho ideálnu prenosovú
funkciu a metódy pre adaptívne riadenie neceločíselného rádu,
v) metódy pre implementáciu regulátorov neceločíselného rádu v analógovej i v digitálnej podobe.
Využívanie regulátorov neceločíselného rádu v riadení má v anglickom jazyku ustálené slovné spojenie „Fractional control“. Ak by sme ho chceli zaradiť medzi existujúce spôsoby riadenia vzhľadom na neurčitosť parametrov riadenej sústavy, poruchy pôsobiace na sústavu a inteligenciu riadenia, môžeme to urobiť tak, ako je to znázornené na obrázku. Výsledky prác ukazujú, že ide o riadenie, ktoré je dostatočne robustné a veľmi vhodné, pretože využíva niektoré vlastnosti derivácie a integrálu neceločíselného rádu, ako je napríklad pamäťový efekt a ďalší stupeň voľnosti.
http://people.tuke.sk/ivo.petras/
https://www.amazon.com/Ivo-Petr%C3%A1s/e/B004N7Y4GM/
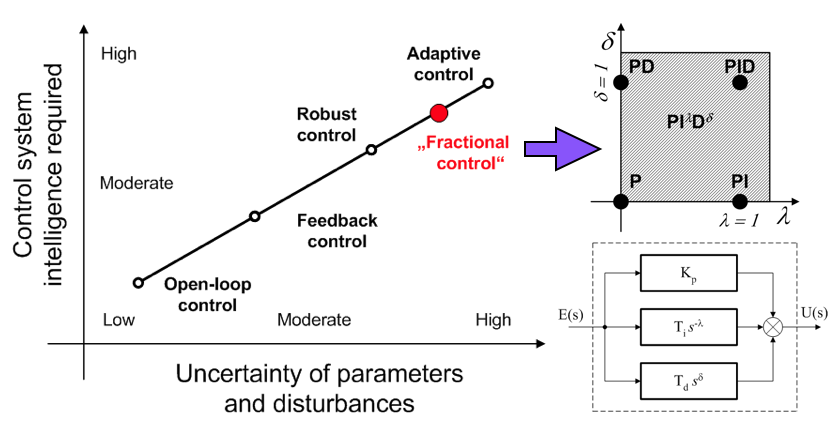
V priemyselných aplikáciách sa stále vo veľkej miere využívajú Proporcionálno-Integračno-Derivačné (PID) regulátory. Riadiace algoritmy založené na PID regulátoroch patria teda stále medzi najpopulárnejšie. Táto popularita spočíva hlavne v ich efektívnosti a funkčnej jednoduchosti. Klasický tvar PID regulátora je možné zovšeobecniť na regulátor, ktorý bude mať neceločíselný rád pri integračnej a derivačnej zložke. Týmto zovšeobecnením dostávame PID regulátor neceločíselného rádu a týmto aj nový spôsob riadenia (Fractional control).
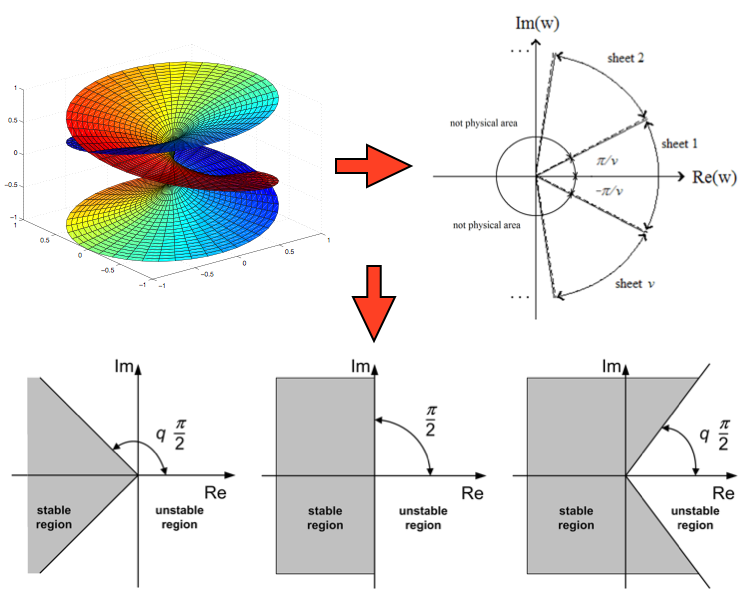
Klasické metódy vyšetrovania stability, ako napríklad Routhovo-Hurwitzovo kritérium, nemôžu byť vzhľadom na reálny rád systému použité, preto bolo potrebné nájsť iné postupy. Hlavnou príčinou je to, že pri systéme neceločíselného rádu dostávame namiesto polynómu n-tého stupňa takzvaný pseudopolynóm, ktorý je mnohoznačnou funkciou. Korene takejto funkcie ležia na Riemannových listoch, ktoré tvoria Riemannovu plochu. Ich hľadanie už nie je triviálne. Prvý Riemannov list je najdôležitejší, pretože iba korene ležiace na tomto liste majú vplyv na stabilitu systému. Je nutné poznamenať, že mapovanie prvého Riemannovho listu do Gaussovej komplexnej roviny sa robí pomocou transformácie. Z uvedeného vyplýva, že stabilná oblasť v Gaussovej komplexnej rovine potom nie je jej ľavá polovica, ale je to výsek daný transformačným vzťahom. Je samozrejmé, že pre q = 1 dostaneme klasický prípad.
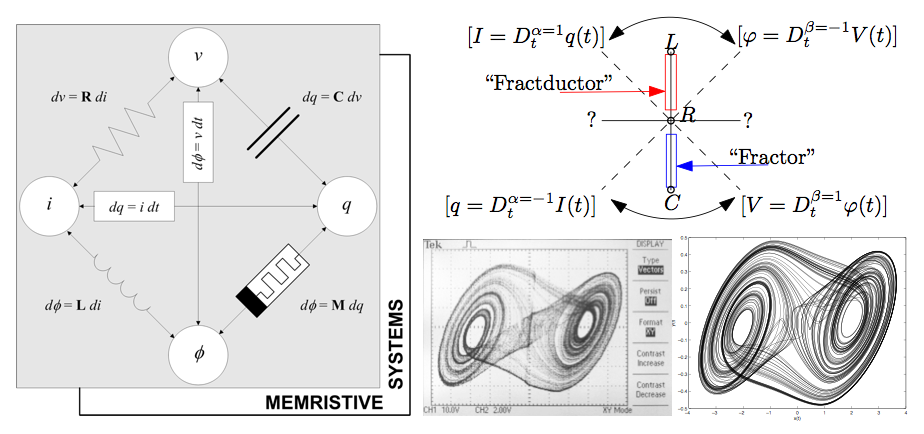
Počas výskumu bolo preukázané, že matematické modely neceločíselného rádu sú adekvátnejšie ako klasické a lepšie opisujú reálne správanie systému. Príkladom sú modely elektrických obvodov, napríklad aj veľmi známeho systému, takzvanému Chuovho systému neceločíselného rádu. Po prvýkrát bol odvodený model, kde sa prirodzenou cestou objavili diferenciálne rovnice neceločíselného rádu, pretože ako matematické modely jednotlivých súčiastok použitých v Chuovom obvode boli uvažované nové tvary využívajúce derivácie neceločíselného rádu. Verifikácia reálnych meraní na osciloskope a numerických simulácií potvrdila dobrú zhodu matematického modelu s realitou.
 Učená spoločnosť Slovenska
Učená spoločnosť Slovenska