Učená spoločnosť Slovenska 
Príspevky členov Učenej spoločnosti Slovenska
Modelovanie komplexných javov v neklasických kontinuálnych prostrediach
prof. RNDr. Vladimír Sládek, DrSc.
Ústav stavebníctva a architektúry SAV
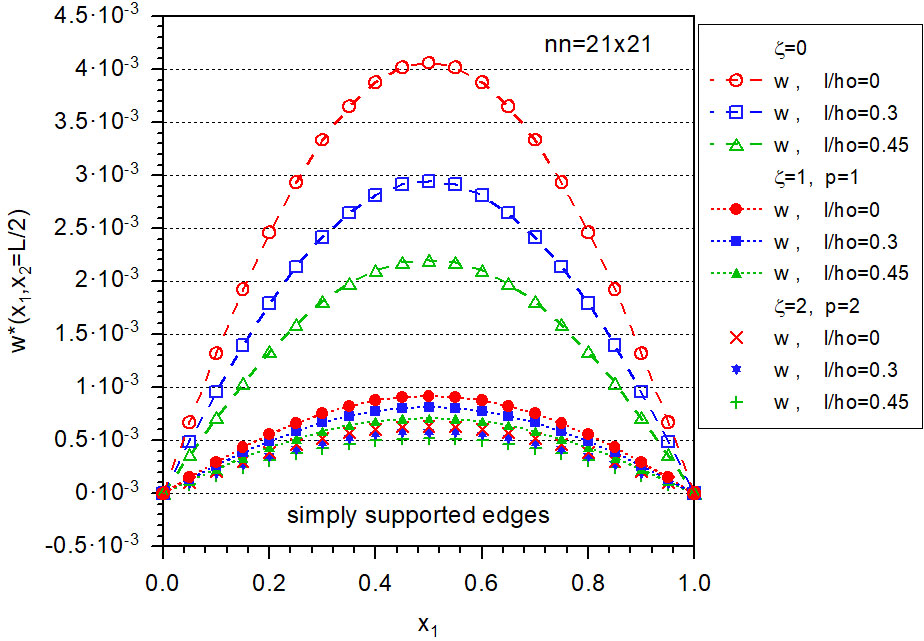
Výskum je zameraný na matematické modelovanie komplexných javov, vznikajúcich v kontinuálnych prostrediach v dôsledku interakcií rôznych fyzikálnych polí. V našom vývoji progresívnych numerických výpočtových metód je možné vyčleniť 2 základné etapy, hoci ich spoločnou črtou je, že patria do skupiny tzv. „mesh reduction methods“ (dikretizačné metódy s redukovanou sieťou). V 1. etape sme prispeli k vývoju regularizovaných hraničných integrálnych rovníc v metóde hraničných elementov, a v 2. etape sme sa zamerali na vývoj a aplikácie diskretizačných výpočtových metód s bezprvkovými aproximáciami poľných premenných. Vďaka takýmto metódam je možné prekonávať niektoré nedostatky klasických numerických výpočtových metód (ako napr. metódy konečných diferencií, metódy konečných prvkov) a aplikovať ich aj na okrajovo-počiatočné úlohy s riadiacimi rovnicami v tvare systémov parciálnych diferenciálnych rovníc s premennými koeficientami. Jednou z aplikácií je štúdium ohybu dosiek, pre ktoré existuje viacero teórií s ich použiteľnosťou v závislosti od hrúbky dosky. Z hľadiska numerických výpočtov je vhodné mať jednotnú teóriu na opis interakčných javov v doskách, umožňujúcu použitie jedného výpočtového programu, čo sa nám podarilo dosiahnúť. Prudký rozvoj materiálového výskumu a technologický progres v spojení s miniaturizáciou vyžadujú modelovanie javov v rámci neklasických teórií kontinua (napr. uvažovanie konštrukcií z funkcionálne gradovaných materiálov, alebo zohľadnenie experimentálne pozorovaných „size effects“, t.j. efektov zavislých od vzájomného pomeru veľkosti konštrukčných prvkov a charakteristickej dĺžky materiálovej štruktúry). Obrázky sú ilustráciou „size“ efektu a vplyvu gradovania Youngovho modulu na priehyby elastických dosiek.
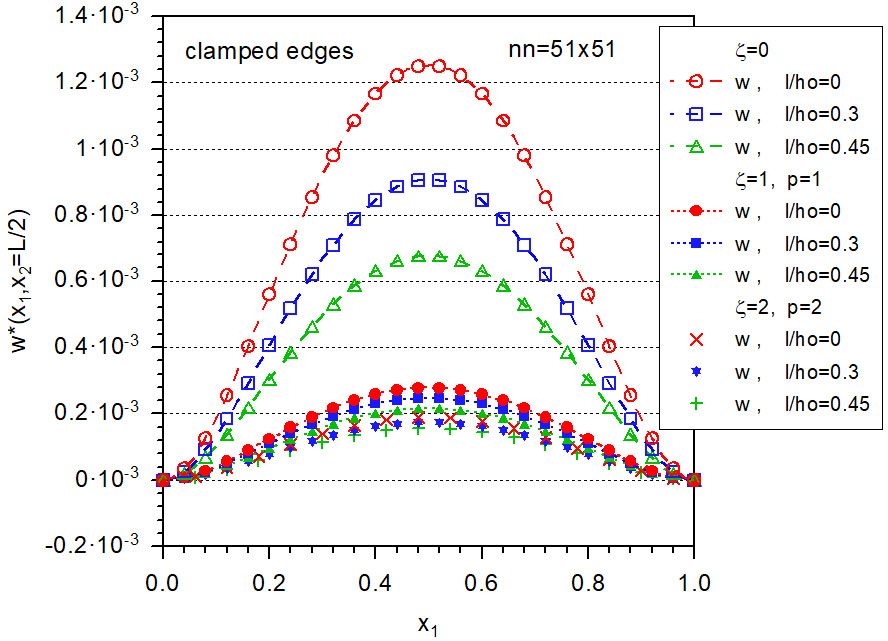
Distribution of deflections along the mid-line in square plates with simply supported edges
and clamped edges for various gradations of Young’s modulus (zeta and p parameters) and various values
of the l/ho-factor (l is micro-length scale parameter, ho is plate thickness)