Príspevky členov Učenej spoločnosti Slovenska
Derivácie a integrály neceločíselného rádu a ich aplikácie
prof. RNDr. Igor Podlubný, DrSc.
Technická univerzita v Košiciach, Fakulta baníctva, ekológie, riadenia a geotechnológií
Táto oblasť, známa pod zaužívaným anglickým názvom “fractional calculus”, predstavuje rýchlo sa rozvíjajúcu oblasť výskumu a aplikácií. Je to spôsobené tým, že aktuálne potreby matematického modelovania a riadenia procesov vedú k požiadavkám na dosiahnutie vyššej adekvátnosti matematických modelov procesov a systémov. Zvlášť výrazne sa táto požiadavka prejavuje pri modelovaní väzkopružných materiálov, pri modelovaní elektrických vlastností polymérov a z nich vyrábaných elektrických súčiastok, pri modelovaní takzvanej anomálnej difúzie v jej rôznych podobách, pri modelovaní mechanických a elektrických vlastností biologických materiálov a vo viacerých iných oblastiach.
Rozvoj aplikácií si vyžadoval tak usporiadanie existujúcich ako aj vývoj nových metód a prostriedkov, a tiež ich spojenie do jasného a zrozumiteľného systému, ktorý by bol použiteľný z hľadiska vedcov a inžinierov z rôznych odborov.
Objasnenie vzťahov medzi rôznymi definíciami derivácií ľubovoľného reálneho rádu prispelo k prudkému rozvoju rozmanitých aplikácií.
Metóda Laplaceovej transformácie s využitím Mittag-Lefflerových funkcií a metóda Greenových funkcií pre diferenciálne rovnice neceločíselného rádu sa stali štandardnými prostriedkami.
Princíp krátkej pamäti sa štandardne používa pri numerických výpočtoch derivácií ľubovoľného reálneho rádu a pri riešení diferenciálnych rovníc s takými deriváciami.
Maticový prístup k diskretizácii derivácií a integrálov ľubovoľného reálneho rádu predstavuje jednotný rámec pre používanie diferenčných schém pri numerickom riešení obyčajných a parciálnych diferenciálnych rovníc tak celočíselného, ako aj neceločíselného rádu.
Navrhnuté PI-lambda-D-mu-regulátory sú ucelenou ilustráciou aplikácie rozpracovaných nástrojov a jedným zo súčasných smerov v oblasti automatického riadenia.
Mittag-Lefflerova stabilita dynamických sústav ľubovoľného reálneho rádu predstavuje nový smer v oblasti zovšeobecnenia klasickej teórie stability.
https://scholar.google.com/citations?user=4H2CInEAAAAJ&hl=en
https://www.amazon.com/Igor-Podlubny/e/B001JS08VS
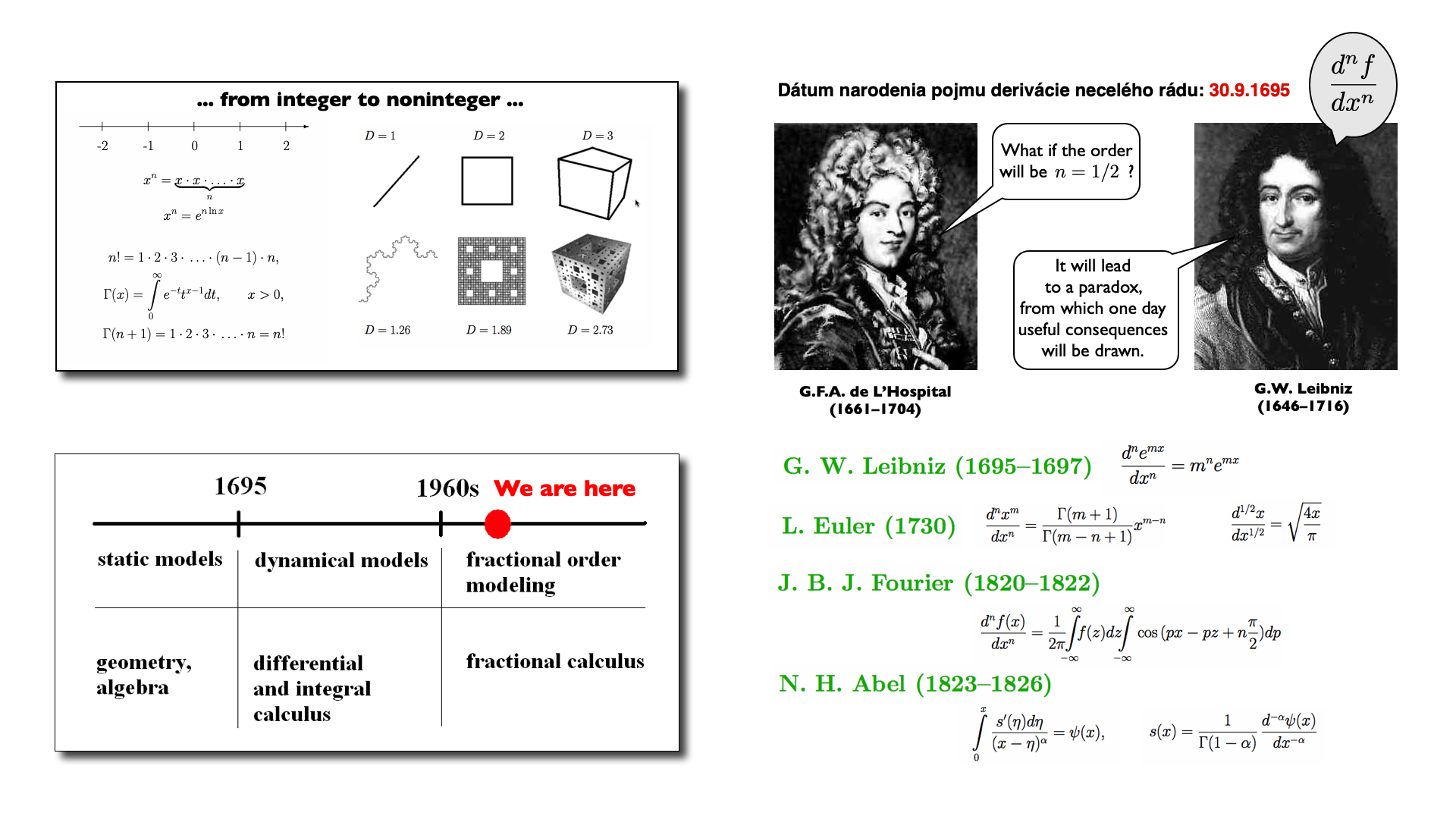
Základná myšlienka – od celého k necelému, od celočíselného k neceločíselnému.
Rozvoj matematických metód je v zásade reakciou na potreby rozvoja vedy a techniky.
Prvá zmienka o derivovaní neceločíselného rádu sa vyskytla už 30. septembra 1695.
K rozvoju koncepcie derivácií neceločíselného rádu prispeli aj Leibniz, Euler, Fourier, Abel, Liouville, atď.
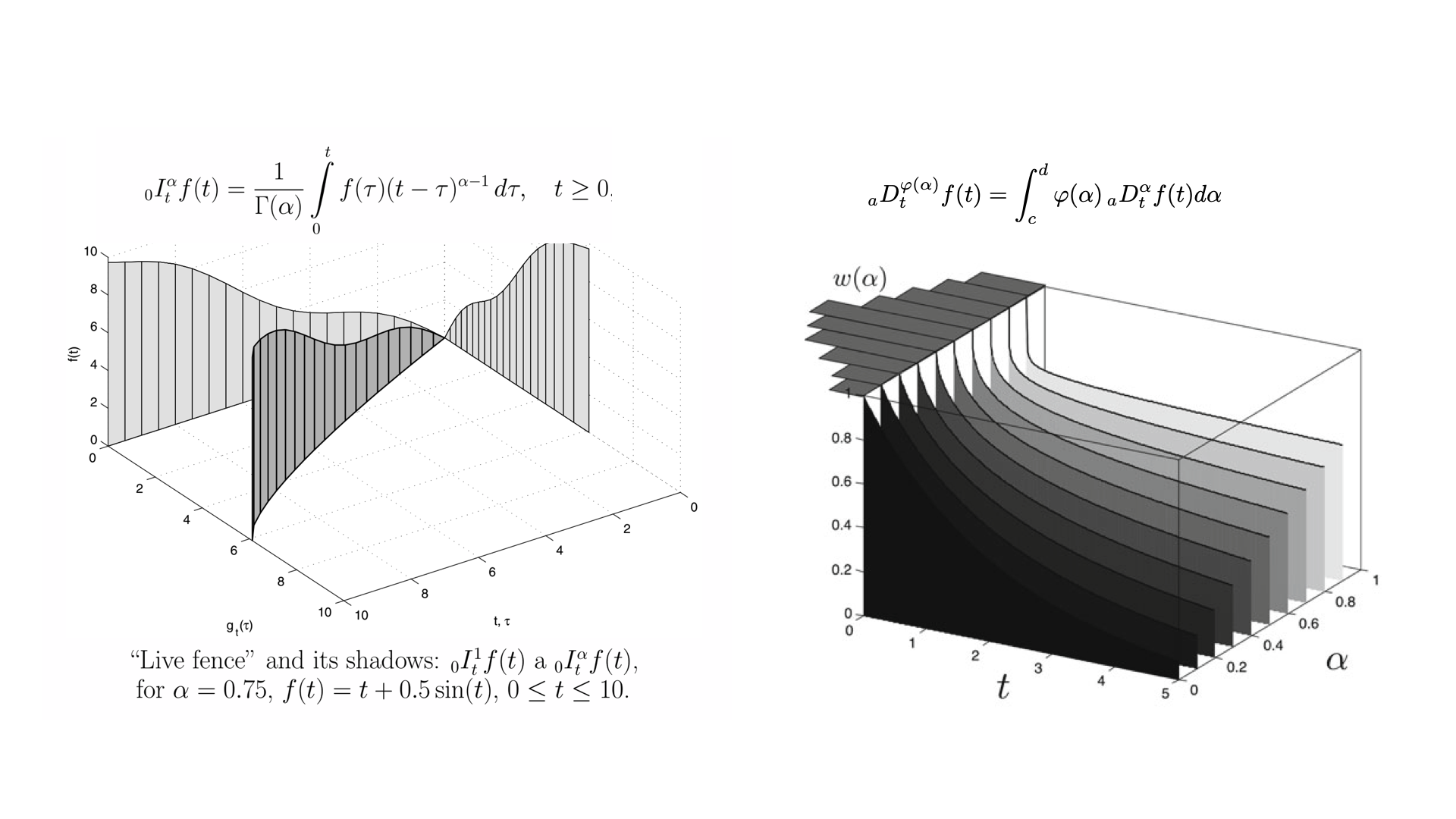
Geometrická interpretácia integrálu neceločíselného rádu (“shadows on the walls”) bola rozpracovaná až po viac ako 300 rokoch (Podlubný, 2002). O desať rokov neskôr bola rozpracovaná aj interpretácia derivácie distribuovaného rádu (Podlubný et al., 2012).
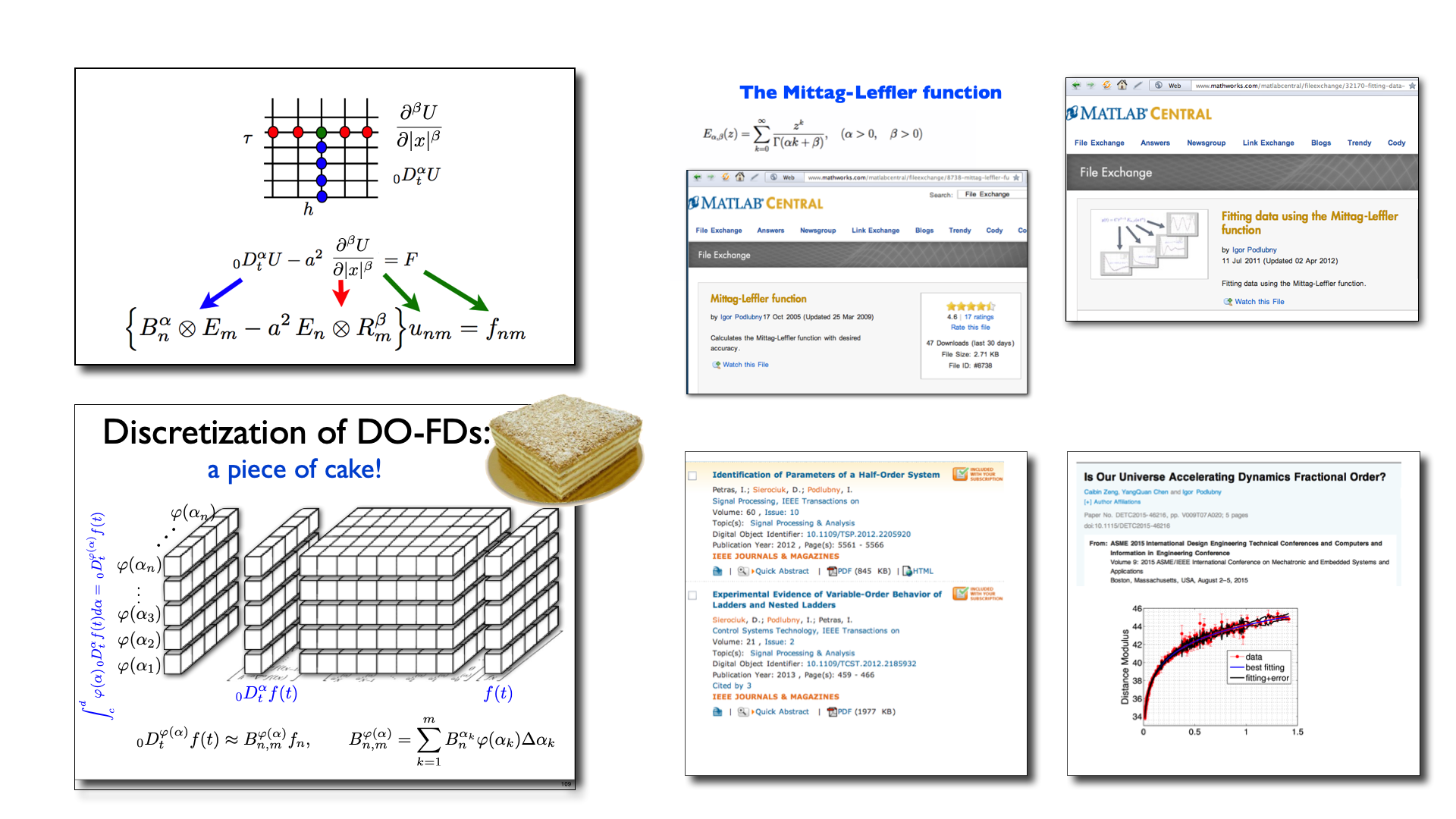
“Matrix approach” (Podlubný, 2000; Podlubný et al., 2009, 2013) je veľmi názornou a ľahko použiteľnou metódou na numerické riešenie rôznych typov obyčajných a parciálnych diferenciálnych rovníc ľubovoľného reálneho rádu, premenlivého rádu a distribuovaného rádu. Použítie Mittag-Lefflerovej funkcie pre identifikáciu parametrov modelov umožňuje tvorbu modelov neceločíselného rádu na základe experimentálnych dát.
 Učená spoločnosť Slovenska
Učená spoločnosť Slovenska